DPP (Determinantal point process) 是一种概率模型,其描述了在全集中进行子集抽样的分布。本文主要介绍DPP算法在推荐系统中的应用,由Hulu公司在NIPS 2018会议上发表的论文‘Fast Greedy MAP Inference for Determinantal Point Process to Improve Recommendation Diversity‘中提出。本文中的DPP均指应用在推荐领域中的概念。
DPP的目的是什么?
对于给定的商品候选列表,兼顾相关性以及多样性的选出一个商品子集。
怎样做到兼顾相关性及多样性?
每个item都有标准化后的representation vector $\mathbf{f}_i$($|\mathbf{f_i}|_2^2=1$),以及一个相关性分$r_i$。相关性分可以理解为就是pointwise模型预测出的得分,如$r_i=0.7$。
定义矩阵$\mathbf{B}$,其中列向量$\mathbf{B_i}=r_i*\mathbf{f_i}$,表示相关分与标准化后的representation vector相乘后的表示向量。
基于矩阵$\mathbf{B}$构建Kernel Matrix $\mathbf{L}$。这里的$\mathbf{L}$中的元素$\mathbf{L_{ij}=\langle\mathbf{B_i},\mathbf{B_j}\rangle}=r_ir_j\mathbf{f_i^T}\mathbf{f_j}=r_ir_j\mathbf{S_{ij}}$,其中,$\mathbf{S}$是根据item标准化表示向量计算出的相似度矩阵。进一步的,kernel Matrix可以表示为$\mathbf{L}=\mathbf{B}\mathbf{B^T}= diag(\mathbf{r}_u)\cdot\mathbf{S}\cdot diag(\mathbf{r}_u)$
为什么Kernel Matrix可以同时衡量相关性和多样性呢?
答案就藏在行列式里。
假设系统给用户u推出的商品集为$R_u$。我们计算Kernal Matrix $\mathbf{L}$的行列式并取log,得到:
等式右边第一项表示整个子集相关分的大小。而等式右边第二项表示多样性的大小。
为什么呢?第一项理解起来比较容易,这里不细讲了。
第二项中的$\mathbf{S}_{R_u}$是商品集$R_u$相似度矩阵,$\mathbf{S}_{R_u}=\mathbf{F}_{R_u}^{\mathbf{}T}\mathbf{F}_{R_u}$,其中$\mathbf{F}\in \mathbf{R}^{N*M}$,$N$表示item representation vector的维度,$M$表示item数。由行列式的乘法定理可知,当$A$与$B$为维度相同的方阵时,$det(AB)=det(A)det(B)$。所以,
矩阵$\mathbf{A}$行列式的物理含义是:以$\mathbf{A}$的列向量为张量,张成多边体的体积。对于二维矩阵,行列式等于张成多边形的面积。如下图所示。
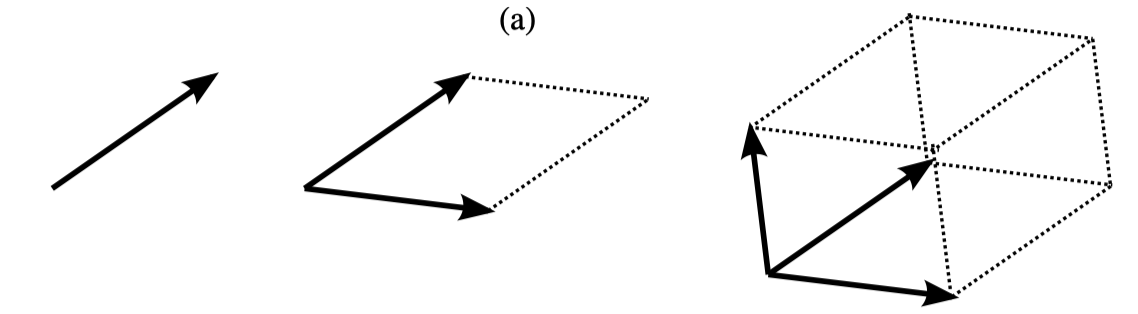
所以$det(\mathbf{S}_{R_u})=Vol^2(\mathbf{F}_{R_u})$,其中,$Vol(\mathbf{F}_{R_u})$表示$\mathbf{F}_{R_u}$张成的体积。当多边体形成立方体时,体积最大,这时$R_u$列表中的item表示向量都是正交的。正交就意味着两个item的相似度为0。当然这是理想情况,这也说明了行列式越大,多样性越好,为衡量多样性提供了依据。
综上,通过计算$\mathbf{L}_{R_u}$的行列式,可以同时衡量相关性和多样性。
如何求解$R_u$?
Hulu提出的方法,利用DPP进行多样性调整,本质上就是利用构造出来的Kernal Matrix,在每轮迭代中,选出使对应行列式增加最多的单个item,直到满足迭代停止条件。这是一种贪心迭代算法,所以最终求得的结果是局部最优。
也就是说,从结果集$Y_g=\{\}$开始,每次选取item j使得结果集$Y_g\cup{j}$的kernel matrix$\mathbf{L}_{Yg\cup j}$的行列式相较于$\mathbf{L}_{Y_g}$提升最大,即:
具体的算法流程如下:

在实际的推荐场景中,用户往往在一屏中会看到固定个数的item,当用户产生下滑行为时,这时的多样性其实是滑动窗口(sliding window)内的多样性。具体的算法流程如下:

当然,上述流程的背后其实有数学理论支撑。由于本篇文章篇幅有限,有兴趣的小伙伴可以阅读原论文进行深入的理解。